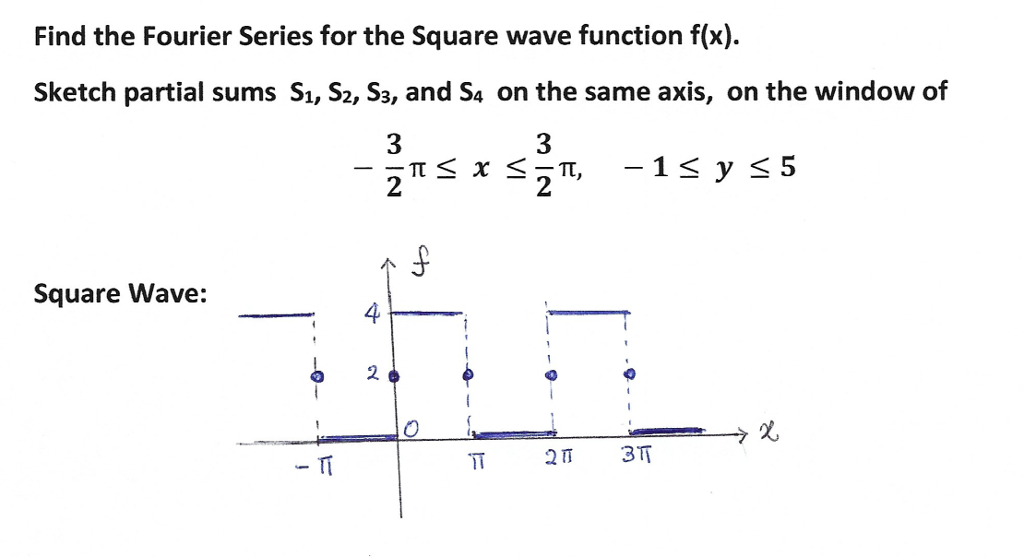
Fine Beautiful Tips About What Is The Square Of Wave Function

Unveiling the Quantum World

1. Deciphering the Quantum Mystery

Alright, let's talk about the square of the wave function. Sounds intimidating, right? Like something straight out of a sci-fi movie where theyre warping space and time. Actually, its way more fundamental than that — it's basically the key to understanding where a tiny particle, like an electron, is likely to be hanging out. Imagine playing hide-and-seek with something invisible. The square of the wave function is your detective's flashlight, illuminating the areas with the highest chances of finding your elusive friend.

Think of it this way: the wave function itself is this complex mathematical description of a particle's state. It's not a physical wave in the way we think of water waves or sound waves. It's more like a probability map. Now, squaring this wave function takes that probability map and turns it into a probability density. This density tells us the probability of finding the particle within a specific tiny volume of space.

So, if you calculate the square of the wave function and find a big number in one spot, that means "Hot diggity dog! The electron is probably chilling right HERE!" If it's a small number, well, the electron is likely vacationing somewhere else. It's not an exact location, mind you — quantum mechanics is all about probabilities, not certainties. Its a bit like predicting the weather; you can say there's an 80% chance of rain, but you can't guarantee it.

One of the coolest things is how this helps explain phenomena like quantum tunneling. An electron might have a chance of being on the other side of a barrier, even if it doesn't have enough energy to classically "climb" over it. It's like it's burrowing through the wall. The square of the wave function shows us that there's a non-zero probability of finding it there, even if it seems impossible!

From Wave Function to Reality

2. Making Sense of Probability Density

Okay, lets dive a little deeper into this whole probability density thing. The square of the wave function, often denoted as ||, gives us a number that represents the likelihood of finding a particle at a specific point in space. It's not just a random number; it's carefully calculated based on the wave function, which incorporates all the information about the particle's energy, momentum, and other properties.

Imagine you're designing a new type of solar panel, and you need to know where the electrons are most likely to be located within the material. This is where the square of the wave function comes into play. By calculating the probability density, you can optimize the panel's design to maximize the capture of light and generate more electricity. Pretty neat, huh?

Another excellent analogy is thinking about a cloud. You can see the cloud, but you can't pinpoint the exact location of every single water molecule within it. The square of the wave function is similar; it tells us where the particle is likely to be, based on the cloud's overall shape and density. Where the cloud is thickest (highest density), you are most likely to find water molecules.

It's important to note that the total probability of finding the particle somewhere must equal 1. This means that if you were to integrate the square of the wave function over all of space, you'd get 1. In essence, this just means that the particle exists somewhere! Its not going to vanish into thin air (well, not usually, anyway — thats a whole other quantum can of worms).

The Significance of Measurement

3. What Happens When We Look?

This is where things get really weird (and fascinating). Before we measure the position of the particle, it exists in a superposition of states, meaning it has a probability of being in multiple places at once. Its like a blurry, smeared-out existence governed by the wave function. But the moment we try to measure its position, the wave function "collapses," and the particle suddenly appears in one specific location. Boom! Reality sets in.

Think of Schrdinger's Cat — is it dead or alive? Before we open the box, it's both! It exists in a superposition of dead and alive states. Only when we open the box and observe the cat does its state collapse into one or the other. The square of the wave function helps us understand the probabilities before the box is opened.

This whole collapse thing has been a source of debate among physicists for decades. Some believe that consciousness plays a role in collapsing the wave function, while others think it's simply a consequence of the interaction between the quantum system and the measuring apparatus. Whatever the explanation, it's a profound concept that challenges our classical intuitions about the nature of reality. It is a subject of continuous study.

Its like flipping a coin. Before it lands, it's in a superposition of heads and tails. Once it lands, the superposition collapses, and you get either heads or tails. The probability of each outcome is determined by the initial conditions (how you flipped the coin), just like the square of the wave function determines the probabilities of different locations for a particle.

Applications in Quantum Technologies

4. Where Does This Quantum Stuff Show Up?

So, all this talk about wave functions and probabilities might seem a bit abstract. But guess what? It has real-world applications that are revolutionizing technology. Quantum computers, for example, leverage the principles of superposition and entanglement to perform calculations that are impossible for classical computers. And guess what's at the heart of it all? Yep, the wave function and its square!

Quantum cryptography relies on the laws of quantum mechanics to ensure secure communication. One key principle is the fact that any attempt to eavesdrop on a quantum communication channel will inevitably disturb the quantum state, alerting the sender and receiver to the presence of an eavesdropper. The probability of detecting such an attempt can be calculated thanks to our friend, the squared wave function.

Furthermore, understanding and manipulating quantum systems is crucial for developing new materials with exotic properties, such as superconductors that can conduct electricity with no resistance, or topological insulators that can conduct electricity only on their surfaces. The wave function and its square are essential tools for predicting and understanding the behavior of electrons in these materials.

Even medical imaging techniques like MRI (magnetic resonance imaging) rely on understanding the quantum properties of atoms. By manipulating the spins of atomic nuclei, we can create detailed images of the inside of the human body. The square of the wave function helps us understand how these spins interact with magnetic fields, allowing us to optimize the imaging process.

FAQ

5. Frequently Asked Questions

Let's tackle some of the questions that might be swirling around in your head right now:

Q: Is the square of the wave function a real, physical thing?

A:

No, it's not a physical object. It's a mathematical tool that helps us understand the probability of finding a particle in a specific location. It's a bit like a map — the map isn't the territory, but it helps you navigate the territory.

Q: Can I use the square of the wave function to predict the exact location of a particle?

A:

Nope! Quantum mechanics is inherently probabilistic. The square of the wave function only gives you the probability density, not the exact location. You can only say that the particle is likely to be in a certain region of space.

Q: What happens if I don't square the wave function? What does just the wave function by itself mean?

A:

The wave function itself can be a complex number, including an imaginary part. Squaring it (or, more precisely, multiplying it by its complex conjugate) ensures that the result is a real number, which can then be interpreted as a probability density. The wave function itself holds information about the phase of the particle, which is important for understanding phenomena like interference.