Lessons I Learned From Tips About What Is The Formula For 3-phase Current

Demystifying the 3-Phase Current Formula

1. Understanding the Basics

Alright, let's talk 3-phase current. It sounds intimidating, right? Like something only electrical engineers understand. But honestly, it's not as scary as it seems. Think of it as electricitys way of being super efficient and delivering power smoothly. We're going to break down the formula for 3-phase current so that even if youre not an electrician, you can still grasp the concept.

In a nutshell, 3-phase power is a system where three alternating currents are supplied, each out of phase with the others by 120 electrical degrees. This setup provides a more consistent and powerful supply compared to single-phase systems, which you usually find in homes. Its why factories, large buildings, and other places with high power demands rely on 3-phase.

Before we dive into the actual formula, let's quickly touch on why we even need to calculate 3-phase current. Understanding the current flowing in a system is crucial for several reasons: safety (avoiding overloads and fires!), choosing the right size wires and equipment, and generally making sure everything runs as intended. So, yeah, it's pretty important.

Think of it like this: you wouldn't just blindly pour ingredients into a cake without measuring, would you? Same goes for electricity. The formula helps us measure and control the "ingredients" so we can "bake" a stable and reliable power system. Now, let's get cooking!

The Magic Formula(s)

2. Two Flavors of Current

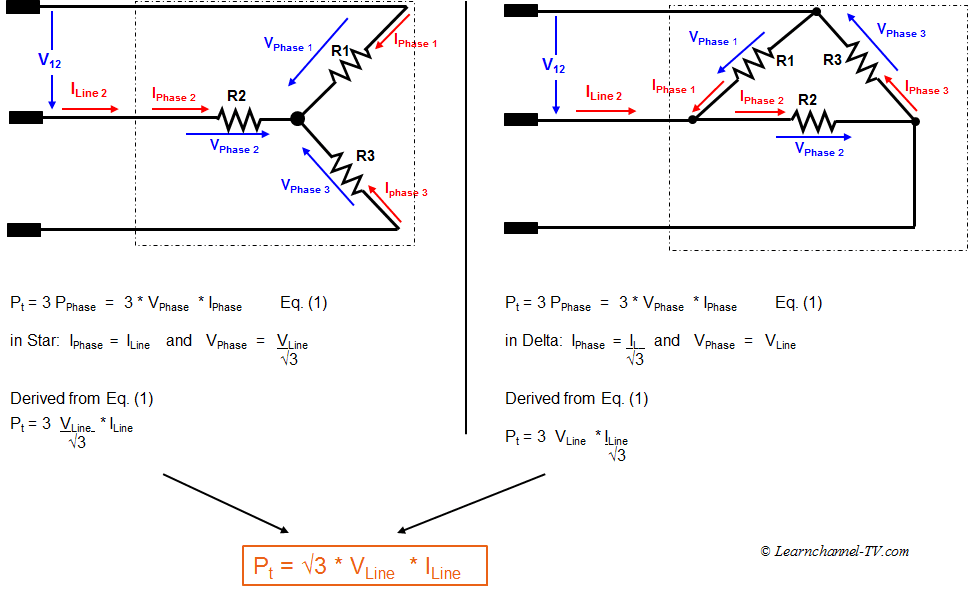
Okay, so there isnt just ONE formula. Like a good recipe, there are a couple, depending on what you need to find out. Weve got two main types of current to consider in a 3-phase system: line current (I_L) and phase current (I_P). The difference between them depends on whether the system is connected in a "star" (also known as "wye") or a "delta" configuration.

In a star (or wye) connection, the line current is equal to the phase current. Simple, right? I_L = I_P. The formula to calculate current depends on the voltage and power. Let's imagine we have a three phase wye connection that needs to supply a motor; to find the I_L, we'd need the power (P), voltage (V), and power factor (PF) of the motor. Then we can apply the equation I_L = P / (3 V PF).

But wait, what's a power factor? Power factor (PF) is a measure of how effectively electrical power is being used. Ideally, it's close to 1, meaning the power is being used efficiently. A lower power factor means more power is being wasted, which can lead to higher energy bills and system inefficiencies. The power factor is usually specified by the manufacture of the load; you can typically find it printed on the nameplate. If there is no nameplate, you'll have to measure it!

For a delta connection, things get a bit trickier. In this case, the line current is not the same as the phase current. It's related by the square root of 3 (approximately 1.732). The relationship is: I_L = 3 I_P. This means the line current is about 1.732 times greater than the phase current in a delta connection. Just like before, to actually calculate the I_P, we'd use the same power, voltage, and power factor equation as before: I_L = P / (3 V PF). Then, to find the phase current, just divide the line current by 3 !

Dissecting the Formula: A Deep Dive

3. Peeling Back the Layers

Let's break down the core formula we've been hinting at, step by step. The most common formula youll encounter for calculating 3-phase current is derived from the power equation:

P = 3 V_L I_L PF

Where:

• P is the power in watts (W)
• V_L is the line voltage in volts (V)
• I_L is the line current in amperes (A) — this is what we're usually trying to find!
• PF is the power factor (a dimensionless number between 0 and 1)

To find the line current (I_L), we simply rearrange the formula:

I_L = P / (3 V_L PF)

So, to use this formula, you need to know the power (P) being consumed by the load, the line voltage (V_L) of the 3-phase system, and the power factor (PF) of the load. Let's say we have a 3-phase motor that consumes 10,000 watts (10 kW), is connected to a 480V system, and has a power factor of 0.8. Plugging these values into the formula, we get: I_L = 10000 / (3 480 0.8) 15.04 amps. Therefore, the line current is approximately 15.04 amps.

Real-World Examples

4. From Theory to Reality

Alright, let's ditch the hypothetical and look at some concrete examples of how this formula is used in the real world. Imagine you're an electrician tasked with installing a new 3-phase air conditioning unit in a commercial building. The manufacturer's specifications state that the unit consumes 15 kW of power, operates on a 208V 3-phase system, and has a power factor of 0.9.

Using our formula, I_L = P / (3 V_L PF), we can calculate the line current. Plugging in the values, we get: I_L = 15000 / (3 208 0.9) 46.2 amps. This tells you that you need to select wires and circuit breakers that can safely handle at least 46.2 amps, with some extra margin for safety.

Let's take another example, this time in a factory setting. Suppose a large industrial pump is drawing 25 kW of power from a 480V 3-phase system with a power factor of 0.85. Using the same formula, we find: I_L = 25000 / (3 480 0.85) 35.4 amps. This information is crucial for ensuring the electrical panel and wiring are adequately sized to support the pump's power demand.

These examples highlight the practical importance of understanding and applying the 3-phase current formula. It's not just about crunching numbers; it's about ensuring the safety, reliability, and efficiency of electrical systems in various applications.

Troubleshooting and Common Mistakes

5. Avoiding the Pitfalls

Even with a straightforward formula, mistakes can happen. One common error is using the wrong voltage value. Always double-check whether you're using the line voltage (V_L) or the phase voltage (V_P), especially when dealing with delta connections. Remember, in a delta connection, line voltage and phase voltage are the same, but the line current and phase current are different! The phase current is derived from the impedance of each phase; calculating this is an advanced topic and beyond the scope of this article. However, it is very important for proper troubleshooting.

Another pitfall is neglecting the power factor. Many people assume a power factor of 1, but in reality, most electrical equipment has a power factor less than 1. Ignoring the power factor can lead to significant errors in your current calculations and potentially result in undersized wiring or equipment.

Also, be mindful of units. Make sure you're using consistent units throughout your calculations. Power should be in watts, voltage in volts, and current in amperes. Mixing units can lead to incorrect results. Additionally, double-check the system connection type (star or delta) as it affects the relationship between line and phase currents.

Finally, invest in a good multimeter or clamp meter to measure current directly. While calculations are essential, real-world measurements can provide valuable insights and help you verify your calculations.

FAQ

6. Clearing Up the Confusion

Let's address some common questions about 3-phase current and its formula:

Q: What happens if I use the single-phase current formula on a 3-phase system?

A: Big problems! The single-phase formula doesn't account for the 3 factor and the phase differences in a 3-phase system, leading to significant underestimation of the current. This can result in undersized wiring, overloaded circuits, and potential fire hazards.

Q: Is the power factor always given? What if I don't know it?

A: Ideally, the power factor should be specified on the equipment's nameplate. If it's not, you can use a power analyzer to measure it directly. Alternatively, you can estimate a typical power factor based on the type of load (e.g., 0.8 for motors, 0.95 for lighting). However, for accurate calculations, measuring the power factor is always recommended.

Q: Why is 3-phase power better than single-phase?

A: 3-phase power delivers more consistent power, resulting in smoother operation of motors and equipment. It's also more efficient for transmitting large amounts of power, making it ideal for industrial and commercial applications.

Q: Is there an easy way to remember the formula?

A: Think of it this way: Power equals "3 Vikings In Line with Power Factors," where Vikings represent the Volts (V), the "In Line" represents the Line Current, and the Power Factors stands for Power Factor. It's a bit silly, but it works!